[Pintos] 4.4BSD 스케줄러(4.4BSD Scheduler) - niceness, priority, recent_cpu, load_avg, fixed-point real arithmetic

멀티스레드 프로그램에서는 구조가 상이한 여러 스레드들이 함께 존재한다. 어떤 스레드는 다수의 I/O 요청을 처리하지만 복잡한 연산 작업은 없을 수 있으며, 어떤 스레드는 I/O 요청 없이 다수의 복잡한 연산 작업 만으로 이루어져 있을 수 있다. 위의 첫 번째 스레드는 I/O 장비와의 빠른 반응속도를 필요로 하지만 CPU time 은 거의 필요하지 않지만, 뒤의 스레드는 반대이다. 이렇게 다양한 스레드들이 존재하기 때문에, 효율적인 프로그램을 위해서 Scheduler(스케줄러) 는 이러한 요구들이 최대한 효율적으로 사용되도록 배치해야 한다. 이를 위해 스케줄러는 priority 라는 속성을 관리하는데, 이 속성에 기반하여 스레드들의 처리 순서를 결정한다. 이 포스트에서는 4.4BSD Scheduler 스케줄러가 각 스레드의 priority 를 관리하는 방법을 공부한다.

 

4.4BSD 스케줄러는 multilevel feedback queue scheduler 의 구성을 갖는다. 이러한 방식에서 ready queue 가 여러개 존재하고, 각각의 ready queue 는 서로 다른 priority 를 가진다. 실행중이던 스레드가 실행을 끝내면, 스케줄러는 가장 priority 가 높은 ready queue 에서부터 하나의 스레드를 꺼내와 실행시키고, 해당 ready queue 에 여러 스레드들이 있는 경우 "round robin" 방식으로 스레드들을 실행시킨다.

 

* round robin : 스레드 간에 우선순위를 두지 않고, 순서대로 정해진 시간단위로 CPU 를 할당하는 방식의 스케줄링 알고리즘이다. 시간단위만큼 실행된 스레드는 리스트의 맨 뒤로 이동한다.

 

 

1. Niceness

각 스레드는 이 스레드가 다른 스레드에 대해 어떠한 성질을 가지는지를 나타내는 정수의 nice 값을 가진다. 이 값은 말 그대로 남에게 얼마나 멋있는지의 정도, 즉 남(다른 스레드) 에게 얼마나 자신의 것(CPU time) 을 잘 양보하는지를 나타낸다. nice value 의 범위는 -20 부터 20의 값을 가진다.

• nice value < 0 : 값이 작을수록 자신의 CPU time 을 다른 스레드에게 양보하는 정도가 크다.
• nice value = 0 : 스레드의 priority 에 영향을 끼치지 않는다.
• nice value > 0 : 값이 클수록 다른 스레드의 CPU time 을 더 많이 빼앗아 온다.

 

 

2. Calculating Priority

4.4BSD 스케줄러는 priority 를 0 (PRI_MIN) 부터 64 (PRI_MAX) 의 64개의 값으로 나눈다. 각 priority 별로 ready queue 가 존재하므로 64개의 ready queue 가 존재하며, priority 는 값이 커질수록 우선순위가 높아짐(먼저 실행됨)을 의미한다. 스레드의 priority 는 스레드 생성시에 초기화되고, 4 ticks 의 시간이 흐를때마다 모든 스레드의 priority 가 재계산된다. priority 의 값을 계산하는 식은 아래와 같다.

• priority = PRI_MAX - (recent_cpu / 4) - (nice * 2)

 

recent_cpu 값은 이 스레드가 최근에 cpu 를 얼마나 사용하였는지를 나타내는 값으로, 최근에 사용한 cpu 양이 많을수록 큰 값을 가진다. 이는 오래된 thread 일수록 우선순위를 높게 가져서(recent_cpu 값이 작아짐) 모든 스레드들이 골고루 실행될 수 있게 한다.

 

* priority 는 정수값을 가져야 하므로 계산 시 소수점은 버림한다.

 

 

 

3. Calculating recent_cpu

이번에는 priority 를 계산하는 데 사용되는 recent_cpu 값을 어떻게 계산하는지 알아보자. 각 스레드는 작업 도중에 여러 번 cpu 를 할당받아 작업을 수행하고 이 각각의 cpu 사용은 모두 recent_cpu 값에 영향을 주고 이 값이 클수록 priority 는 낮아진다. 여기서 중요한 점은 더 최근에 사용된 cpu 작업일수록 '가중치' 가 붙는다는 것이다. 예를 들어서 thread A 가 1초가 걸리는 cpu 작업을 5번 연속으로 시행했다고 하면, recent_cpu 값은 가장 최근 작업은 1초를 그대로 반영하고, 바로 전 작업은 0.8, 그 전 작업은 0.64 ... 의 방식으로 일정 비율로 그 반영 비율을 달리한 모든 값의 합으로 결정된다. (recent_cpu = 1 + 0.8 + 0.64 + ..). 이러한 계산식을 '지수가중 이동평균 방식(Exponentially Weighted Moving Average)' 라고 한다.

 

 

* 지수 가중 이동평균(Exponentially Weighted Moving Average)

이 개념은 최근 데이터에 더 많은 영향을 받는 데이터들의 평균 흐름을 계산하기 위한 것으로 최근 데이터에 더 높은 가중치를 준다. 수식으로 표현해보자.

x(t) 의 값은 t 번째 데이터의 지수 가중 이동평균을 나타내고, a 는 하이퍼 파라미터로 최적의 값을 대입해 사용하며, f(t) 는 t 번째 데이터의 값을 나타낸다. 우리의 주제에서 사용될때는 x(t) 는 t 시간에서의 recent_cpu 값, a 는 부패율, f(t) 는 t 시간에서 사용한 cpu 양 정도로 대입하면 될 듯하다.

우선, 수식을 이해하기 위해 상세하게 분석해 보도록 하자. 

 

맨 위의 x(t) 에 대한 식은 x(t-1) 을 아래 식으로 대체해주면 아래와 같이 표현된다.

 

여기서 x(t-2) 를 다시 한 번 대체하여 풀어주어 보자.

 

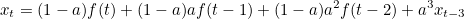
이정도 보면 규칙성이 보일 것 같다. 그대로 쭉 풀어서 쓰면 어떤 식이 나오는지 보자.

 

하이퍼 파라미터인 a 값은 0 과 1 사이의 값으로 사용된다. 0~1 범위의 값은 제곱 할 수록 그 값이 작아지기 때문에, 위의 식의 우변의 항들은 뒤로 갈수록 a 가 한 번씩 곱해져서 그 값의 가중치가 작아진다는 것을 알 수 있다.

 

여기서 한 가지 특징을 더 살펴보자. 각 항의 계수를 보면 등비수열로 이루어져 있다는 것을 알 수 있다. 첫 항은 1-a, 등비는 a 인 등비수열이기 때문에 등비수열의 합 공식을 이용하여 각 계수의 합을 구해볼 수 있다.

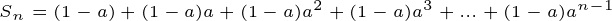
두 식을 빼서 정리하면,

a 의 값이 0 초과, 1 미만의 값이므로 이렇게 정리가 된다. 여기서 모든 항의 합을 구하고자 하였으므로 n 을 무한으로 보내면,

모든 계수의 합이 1 로 가까워진다.

 

x(t) 의 값을 계산할 때마다 모든 데이터 t 에 대한 항을 모두 더하기에는 그 계산이 너무 많아지므로 부패가 많이 진행되어 그 가중치가 일정 수준 이하로 작아진 데이터들은 무시한 근사값으로 계산되는 경우가 많다. 가중치가 1/e (대략 0.37) 이하로 내려갔을 때를 기준으로 다음 항들은 무시한다고 가정해보자. a = 0.9 의 값을 가진다고 하면 a 의 10 거듭제곱의 값이 대략 0.35 로 1/e 와 같으므로 최근 10 개 이전의 데이터들은 그 중요성을 상실하고, a = 0.98 일 경우에는 a 의 50 제곱이 1/e 와 비슷해져서 그 이전 데이터는 무시된다. 이 갯수값은 근사적으로 1/(1-a) 의 값과 같다. (a = 0.9 일 경우 1/(1-0.9) = 10, a = 0.09 일 경우 1/(1-0.09) = 50). 기준이 1/e^2 이라면 {1/(1-a)}^2 값이다.

 

Pintos Document 의 내용에서는 a = k/(k+1) 의 값으로 주어졌으며, 이를 통해 x(t) 를 k 와 연관시킬 수 있다. 바로 위의 내용에서 a 의 거듭제곱이 1/e 의 값과 대략 같아지는 지점이 a 의 1/(1-a) 거듭제곱이라고 했다. a 에 k/(k+1) 을 대입하면 아래와 같다.

위의 식은 대략 k 번의 시간이 흘렀을 때 그 계수가 1/e 이하로 내려감을 보여준다. 이는 t + k 의 시간에 f(t) 의 부패율이 대략 1/e 이 된다는 것과 같은 말이고, 마찬가지로 t + 2k 의 시간에 f(t) 의 부패율이 1/e^2 이하가 된다. 

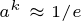
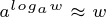
위 식을 통해 f(t) 의 부패율이 w 가 되는데 걸리는 시간은 대략 loga(w) 임을 알 수 있다.

 

적용

'지수 가중 이동평균'의 식은 컴퓨터에서 사용할 때는 주로 아래와 같이 V 의 값을 반복하여 덮어씌우는 방식으로 구현한다.

 

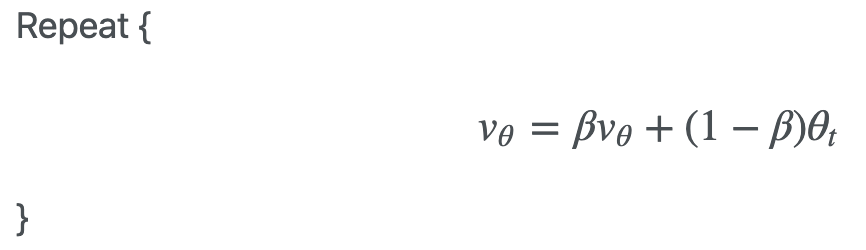
위의 내용을 토대로 recent_cpu 에 적용해보도록 하자. recent_cpu 의 초기값은 init 스레드의 경우에는 '0' 이고, 그 외에는 부모 thread 의 recent_cpu 값을 물려받는다. recent_cpu 의 값은 timer interrupt 가 발생할 때마다 running thread 에서 1 씩 증가하고, 매 1 초마다 모든 therad 에서 재계산된다. pintos 에서 recent_cpu 는 아래와 같이 정의된다.

• recent_cpu = (2 * load_avg) / (2 * load_avg + 1) * recent_cpu + nice

(2*load_avg)/(2*load_avt + 1) 부분을 부패율 a 라고 하고 보면, 처음 생성된 스레드의 경우 위의 규칙에 따라 recent_cpu 의 값이 0, nice, a*nice + nice, a*a*nice + a*nice + nice, ... 로 전개되어 나가는 것을 볼 수 있고, 이는 위에서 공부한 '지수 가중 이동평균' 와 같음을 알 수 있다. 이에 따라 각 시간에서 recent_cpu 의 값을 알 수 있고, 특정 시간의 recent_cpu 값이 특정 부패율이 되는 시간 또한 알 수 있다.

예를 들어, load_avg 값이 1 일 때 현재 recent_cpu 값의 부패율이 0.1 이 되는 시간은 아래의 식에 따라 대략 6초가 걸린다.

 

 

* nice 값이 음수인 경우에 recent_cpu 값이 음수가 될 수도 있다.

* recent_cpu 의 계산과정에서 recent_cpu 의 계수를 먼저 계산하도록 한다. 계수의 계산 전에 recent_cpu 를 곱하는 경우 overflow 가 발생할 수 있다.

 

4. Calculating load_avg

load_avg 값은 최근 1 분동안 수행 가능한(ready to run) 스레드의 평균 개수를 나타내며 recent_cpu 값과 마찬가지로 '지수 가중 이동평균' 을 사용한다. priority, recent_cpu 값은 각 thread 별로 그 값을 가지는 반면 load_avg 는 system-wide 값으로 시스템 내에서 동일한 값을 가진다. load_avg 의 값은 시스템이 부팅될 때 0 으로 초기화되고, 매 1 초마다 아래 식에 따라 업데이트된다.

• load_avg = (59/60)load_avg + (1/60)*ready_threads

ready_threads 값은 업데이트 시점에 ready(running + ready to run) 상태인 스레드의 수를 나타낸다.

 

 

 

5. Fixed-Point Real Arithmetic (고정 소수점 연산)

고정 소수점 VS 부동 소수점 방식

컴퓨터 시스템에서 정수와 다르게 소수점을 포함하는 실수의 표현은 생각보다 훨씬 복잡하다. 그 이유는 컴퓨터가 모든 수를 2진수로 표현하기 때문인데, 이를 해결하기 위해 현재에는 고정 소수점(Fixed-Point) 방식과 부동 소수점(Floating-Point) 방식이 사용된다. 고정 소수점 방식은 말 그대로 소수점의 위치가 고정되어 있다는 뜻이고, 부동 소수점 방식이란 움직이지 않는다는 '부동' 의 의미가 아니라 영어에서 볼 수 있듯이 'floating' 즉 소수점이 고정되어 있지 않고 '떠다니다'(이동한다) 의 의미이다. 

 

간단하게 32bit 를 예로 살펴보면, 고정 소수점 방식에서는 32bit 가 부호 비트, 정수부, 소수부 의 3 부분으로 나누어지고 각각의 bit 수는 시스템에서 정해져있고 변하지 않는다. 다만 정수부와 소수부의 bit 수 개수는 시스템마다 다를 수 있다.

[0 00000000000000000 00000000000000]

• 부호 비트 : 0이면 양수, 1이면 음수를 나타낸다.
• 정수부 : 정수를 표현한다.
• 소수부 : 소수점 이하 자릿수를 나타낸다.

정수부는 일반적인 2진수 계산으로 앞의 bit 로 갈수록 2 씩 곱하여 계산하지만, 소수부는 반대로 2 씩 나누어 계산한다. 아래 표는 정수부 5 bit, 소수부 5 bit 를 예로 각 자리수가 나타내는 값을 표시한다.

0	0	1	0	0	0	1	0	1	0
16	8	4	2	1	0.5	0.25	0.125	0.0625	0.03125

위의 표는 bit 가 1 인 자리의 값을 더하면 되므로, 4.3125 라는 값을 나타낸다.

고정 소수점 방식은 자리수가 적기 때문에 표현할 수 있는 수의 범위가 정수에 비해 현저히 작다.

 

적용

부동 소수점 방식은 표현할 수 있는 범위가 크지만, 계산 시간이 길고 복잡하여 kernel 을 느리게 만들 수 있기 때문에 Pintos 시스템은 부동 소수점 방식은 지원하지 않는다. recent_cpu, load_avg 의 값은 실수로 표현되므로 pintos 에서는 1 bit(부호), 17 bit(정수부), 14 bit(소수부) 를 사용하는 고정 소수점 방식으로 실수를 계산한다.

간단하게 계산하는 방법은, 실제 사용하고자 하는 실수에 2^14 값을 곱하여 사용하면 고정 소수점 방식으로 표현할 수 있다.

예를 들어, 2.75 라는 값을 사용하고자 한다면 2.75 * 2^14 = 45056 의 값을 사용하면 된다.

45056 = [1011000000000000] = [0 00000000000000010 11000000000000] = [+  , 2  , 0.75]

 

주의해야 할 점은 정수와 실수의 표현 방식이 다르기 때문에 연산할 때 보정이 필요하다는 것이다. 정수 + 정수, 실수 + 실수 의 계산처럼 같은 표현 방식을 사용하는 수끼리의 더하기는 아무런 오류가 없지만, 정수 + 실수 의 계산을 하려면 난감해진다.

예를 들어 5 + 2.75 를 계산한다고 하자. 5 는 정수이므로 2 진수로 101 로 표현되지만, 2.75 는 위에서 봤듯이 1011000000000000 이다. 이 경우에는 5 를 실수의 표현 방법으로 변환하여 더하기를 진행히주어야 한다. 즉 5 * 2^14 + 2.75 를 해주면 고정 소수점 방식으로 표현된 올바른 값을 얻을 수 있다. 여러 연산의 방법은 아래 그림으로 첨부한다. (x, y 는 실수, n 은 정수, f 는 2^14 의 값이다.)

 

 

 

 

Reference )

• 지수가중이동평균 : hansololee.github.io/optimization/exponentially_weighted_averages/
• pintos document : web.stanford.edu/class/cs140/projects/pintos/pintos.pdf